- Table of contents
- The Two-Lines Element
The Two-Lines Element¶
TLE¶
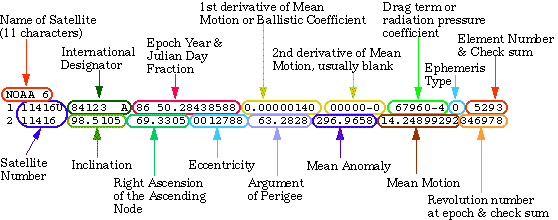
Figure 1 : Two Lines Element
Once the orbit propagator is chosen, some data is required at the input in order to calculate the satellite’s position. This data is stored within the Two Lines Element (TLE). The TLE can be found on the internet but it is important to check if they have been updated lately otherwise precision will be lost in the calculation. TLE are provided by NORAD (North American Aerospace Defence Command).
.
Here is the TLE format (2 lines of 69 characters) :
AAAAAAAAAAAAAAA b.b c.c d.d e.e f RRR KM x km 1 gggggU hhiiijjj kklll.llllllll +mmmmmmmm +nnnnn-n ooooo-o p qqqqr 2 ggggg sss.ssss ttt.tttt uuuuuuu vvv.vvvv ddd.dddd xx.xxxxxxxxyyyyyz
Line 0 description :
AAAAAAAAAAAAAAA : name of the satellite
b.b : length (meters)
c.c : width (meters)
d.d : height (meters)
e.e : standard magnitude
f : standard magnitude determination method (d = calculation ; v = observation)
RRR : equivalent radar section (meter square)
KM : altitude at apogee
km : altitude at perigee
Remark : Most of the time there is no line 0.
Line 1 description :
ggggg : Number within the U. S. Space Command (NORAD)
U : Classification (here U means Unclassified = not secret)
hh : Last two numbers of the lunching year
iii : lunch number of the year
jjj : one to letters pointing a piece of the lunch
kk : two last numbers of the year when these elements have been estimated
lll.llllllll : day and fraction of the day when these elements have been estimated
+ mmmmmmmm : half of the first derivative of the mean movement (revolution per day square), this stands for the acceleration and deceleration of the satellite
+ nnnnn-n : sixth of the second derivative of the mean movement (revolution per day cube)
ooooo-o : pseudo ballistic coefficient, used by the SGP4 orbit propagator (1/terrestrial radius)
This coefficient is also called B-star drag term, it represents the effects of atmopheric drag on the satellite. His unit is in EarthRadii-1.
B*=Cd*r0*A/2*m with Cd : Coefficient of drag r0 : Atmospheric density A : Cross-sectionnal area of the satellite m : Mass of the satellite
p : type of ephemeris
qqqq : number of this set of elements
r : cheksum (modulo 10)
Line 2 description :
ggggg : Number within the U. S. Space Command (NORAD)
sss.ssss : orbit inclination with respect to the terrestrial equator (degrees)
ttt.tttt : right ascension of the orbit ascending node (degrees)
uuuuuuu : excentricity
vvv.vvvv : perigee argument (degrees)
ddd.dddd : mean anomaly (degrees)
xx.xxxxxxxx : mean movement (revolution per day)
yyyyy : number of revolutions when these elements have been estimated
z : cheksum (modulo 10)
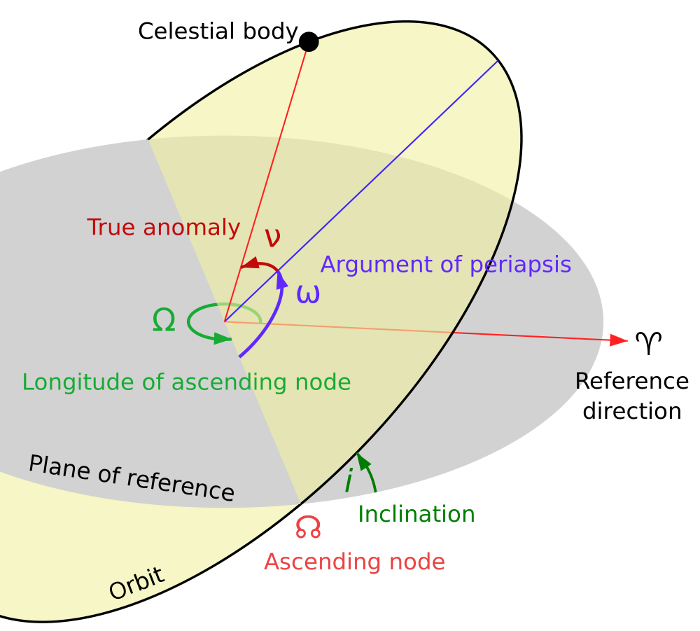
Figure 2 : Orbit Parameters
The previous figure presents the parameters needed to position the satellite on his orbit. These parameters are given in the TLE at the epoch.
Here is an example of a TLE for the NOAA-19 :
1 33591U 09005A 15310.52866608 .00000161 00000-0 11260-3 0 9997 2 33591 99.0081 260.8643 0014724 126.2184 234.0350 14.11998019347577Here are some helpful remarks to interpret the TLE’s values :
- concerning the day and fraction of the day, also called epoch: when these elements have been estimated at line 1, the first two numbers are the last numbers of the year (15 stands for 2015 in the example). The next three numbers designate the number of the day in the year (310 represents November the 6th). Then the last numbers represent the fraction of the day. By multiplying this decimal number by 1440 (the number of minutes in one day), we obtain the time of the day when these elements have been determined. The epoch is the moment where the satellite arrives at the ascending node.
- When there is a « + » before the values, it means that these values can be either positive or negative
- Concerning the excentricity on line 2, the decimal is inherent (0014724 means 0.0014724 in the example)
- Concerning the pseudo-ballistic coefficent on line 1, the decimal is assumed and the last integer represents the minus values at the power of ten (11260-3 stands for 0.11260 x 10^-3)
It is even more important to have updated TLEs for satellite with orbit lower than 350 km that are often subject to maneuver, such as the ISS (International Spatial Station).
References¶
Description of the TLE : http://www.castor2.ca/03_Mechanics/03_TLE/index.html
