Golay code¶

Golay code is a perfect linear error correcting code. It is appeared in 1949 by its inventor Marcel J. E. Golay. At that time, Claude Shannon gave his mark in the information coding by his book The Mathematical Theory of Communication in 1948. The Golay code shows its importance by providing reliability of communication on a noisy channel. Since then, in order to increase the quality and error correction capacity, several encoding and decoding algorithm were done as the algebraic decoding algorithm, the standard array decoding etc..

Knowing that the theory of error detection and correction is deep, we will try to give a simplest idea about the topic without focus a lot on mathematical aspects.

Now, let’s switch on the structure of the binary Golay code.

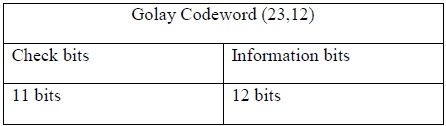
The code word contains 23 bits, shared between 12 information bits and 11 appended check bits which are derived from a modulo-2 division, as with the Cyclic Redundancy Check.
The common notation is Golay (23,12) where 23 refers to the total number of bits and 12 for the information bits. We can then obtain the check bits by the simple subtraction 23-12=11 bits.

This guides to obtain 2^23, or 8,388,608 possible binary values since each codeword is 23 bits long. But, because of that each of the 12-bit information field has only one corresponding set of the 11 check bits, we will have only 2^12, or 4096, valid Golay codewords.
The Golay codeword are spaced from each other by the Hamming distance, which is in our case 7 or more bits. According to this distance, the maximum of error that the Golay code can detect and correct is (d-1)/2=3 bit errors, in any pattern.

References¶

Article Using The Golay Error Detection And Correction Code
http://aqdi.com/articles/using-the-golay-error-detection-and-correction-code-3/