Golay code¶

Golay code is a perfect linear error correcting code. It is appeared in 1949 by its inventor Marcel J. E. Golay. At that time also, Claude Shannon gave his mark in the information coding by his book The Mathematical Theory of Communication in 1948. The Golay code shows its importance by providing reliability of communication on a noisy channel. Since then, in order to increase the quality and error correction capacity, several encoding and decoding algorithm were done as the algebraic decoding algorithm, the standard array decoding etc..

Knowing that the theory of error detection and correction is deep, we will try to give a simplest idea about the topic without focus a lot on mathematical aspects.
To go a little far, we need to be familiar with some definitions in our topic;

Hamming distance: it is the number of bits between two binary numbers.
For example, the Hamming distance between bytes 4Ah and 68h is weight(4Ah XOR 6Fh) = weight(22h) = 2 bits.

Weight: it is the number of ones in a binary word.
For example, the byte word 11001010 has 4 as weight as it contains four 1s.
Now, let’s switch on the structure of the binary Golay code.

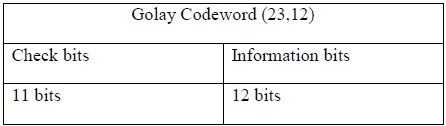
The code word contains 23 bits, shared between 12 information bits and 11 appended check bits which are derived from a modulo-2 division, as with the Cyclic Redundancy Check.
The common notation is Golay (23,12) where 23 refers to the total number of bits and 12 for the information bits. We can then obtain the check bits by the simple subtraction 23-12=11 bits.

This guides to obtain 2^23, or 8,388,608 possible binary values since each codeword is 23 bits long. But, because of that each of the 12-bit information field has only one corresponding set of the 11 check bits, we will have only 212, or 4096, valid Golay codewords.
The Golay codeword are spaced from each other by the Hamming distance, which is in our case 7 or more bits. According to this distance, the maximum of error that the Golay code can detect and correct is (d-1)/2=3 bit errors, in any pattern.

Golay Extended¶

After several attempts to improve this code, Golay Extended code is reached. In this version, we can detect 4-bit errors thanks to adding a parity check bit to the Golay code which allows all combinations of 4 bit errors to be detected but not corrected, and then all odd numbers of bit errors can be detected in codeword. We noted it as Golay (24, 12) and it is used for deep space communication.
Therefore, a trade-off should be taken into account between correct and detect error. Since the maximum number of error detected is 6 in any 24-codeword, 3 bits maximum can be corrected.

So, in any application, depending on what we favorite between error detection or error correction, we get different result;

Error detection case (per 24-bit) in extended Golay

• 100% of one- to six-bit errors detected, any pattern
• 100% of odd bit-errors detected, any pattern
• 99.988% of other errors detected

Using the error correction facilities of the code, these are the data reliability rates:

• 100% of one- to three-bit errors corrected, any pattern
• 100% of four-bit errors detected, any pattern
• 100% of odd numbers of bit errors detected, any pattern
• 0.24% of other errors corrected (1/4096)

References¶

Article Using The Golay Error Detection And Correction Code
http://aqdi.com/articles/using-the-golay-error-detection-and-correction-code-3/

Article IEEE Simplified Algorithm and Hardware Implementation for the (24, 12, 8) Extended Golay Soft
http://www.ccis2k.org/iajit/PDF/vol.11,no.2/4478.pdf