Satellite Link Budget¶
In this section we are going to explain what is a satellite link budget and what are the main parameters it involves.
Satellite Communication System¶
Assuming that a telecommunication system is composed by a transmitter a medium and a receiver, the link budget is the accounting of all gain and losses in the power signal from the transmitter, passing through the medium, to the receiver.So, the link budget analyses how much power is lost in the signal path. With link power analysis it's possible discriminate the value of power loss in each equipment and sub-path.
To easily understand, we can analyse the satellite system showed in figure 1. Considering a signal one-way-travel, just analyzing the individual uplink path, the link budget will perform the power received by the satellite taking in account the amplification and the attenuation of the link.The link, in this case, is composed by the transmitter: the Earth Station, the media: the atmosphere and free space ,and the receiver: the Satellite. Then, in the link budget calculating, we taking in account the following losses and gains:
- Gain of the transmitter and receiver amplifier.
- Attenuation in the atmosphere propagation.
- Depointing losses.
- Polarization mismatch losses.
- Losses in transmitting and receiving equipment.
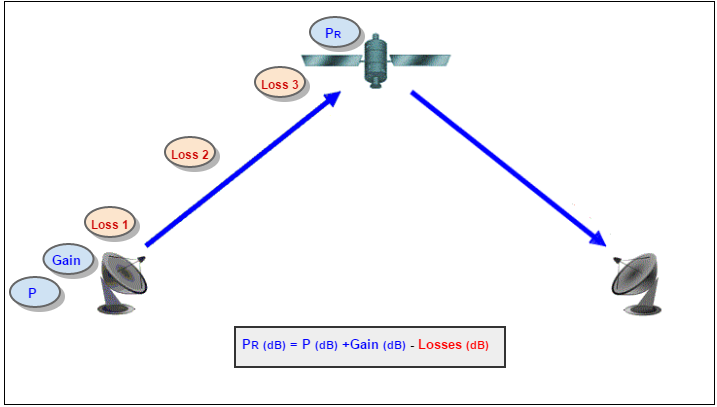
<div style="margin-left: auto; margin-right: auto; width: 50em">Figure 1 - Gain and losses from a signal travelling from a transmitter to a receiver, considering individual uplink path. P is the power before the transmitter amplifier, Gain is the transmitter amplifier gain, PR is the power received, Loss 1 the power lost due to the transmitter equipment, Loss 2 the power lost due to the atmosphere effects, Loss 3 the power lost due to the receiver equipment.
</div>
To evaluate the quality of our link, one important measure is the Bit Error Rate, BER. If we want that our signal maintain a low BER we must to start the transmission with a higher power. We have to be sure that even with all losses along the path way, we'll have enough power available at each point, to keep this BER value.The BER is a function of the bit energy per noise-density of the signal EbNo. The ratio between BER and EbNo depends on the digital modulating implemented. An example of BER x EbNo graphic is showed in figure 2. Higher EbNo means better quality.
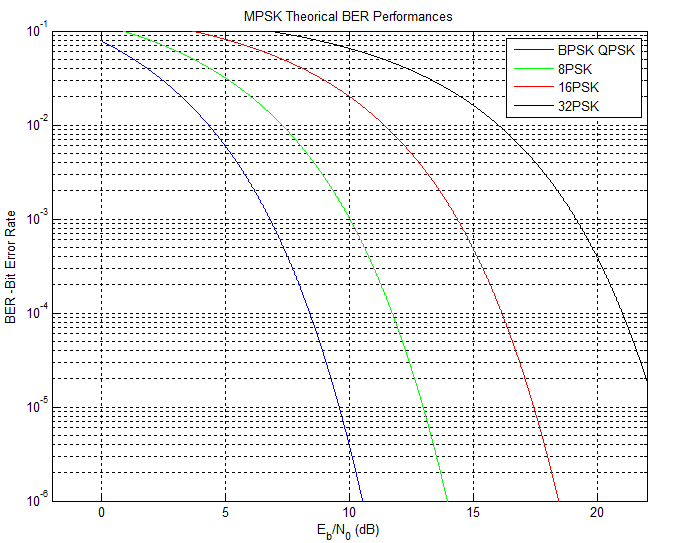
<div style="text-align: center;">Figure 2 - Exemples of BER x EbNo graphics. M-PSK constellations, no coding situation.</div>
- Link performance: Carrier-to-noise power ratio CNo
It's a measure of the power received by receiving equipment, "C", and the noise power density No, introduced in the transmission medium. It is also a measure of the quality of modulated carrier in the receiver input.
- Transmit equipment performance towards receiver: Effective isotropic radiated power EIRP
Is a measure of the power PT and the performance of the transmit equipment in the direction of the receiver. It is expressed in dBW.
- Receiving equipment performance: Figure of merit G/T
The figure of merit is expressed by a ratio between the maximum gain of a receiving antenna to the system equivalent noise temperature.In general it is expressed in dB/K. This relation is also a measure of the ability of the receiver to receive a signal with good quality (high carrier-to-noise ratio).
Figure 3 shows the detailed elements and parameters involved in a satellite link. The transmitter Tx is connected to the antenna by a feeder. The antenna has a gain GT in the receiver direction. The power radiated by the emitter after the feeder loss FFTX is PT. The receiver antenna has a gain GR in the direction of the transmit equipment, connected by a feeder in a receiver equipment Rx. In the receiver input the power received is denoted by C. in the link, all sources of noise contributes to the system noise temperature T. The (C/No)T depends on the system noise temperature (which condition the noyse power spectral density No).
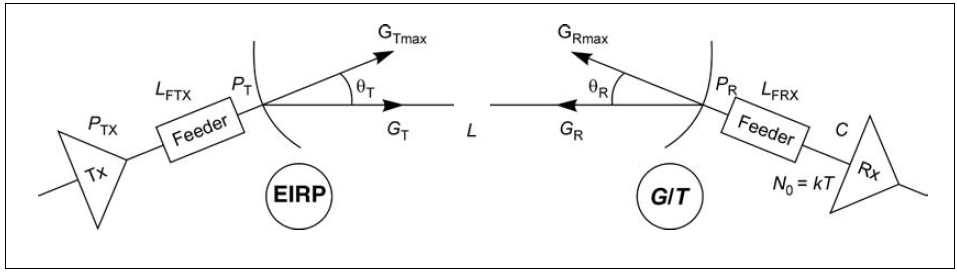
<div style="text-align: center;">Figure 3 - Link configuration.</div>
